元本を複利で運用する計画を立てる場合に、現価係数や終価係数を用いると、必要な元本額や最終的な元利合計額を簡単に求めることができます。
現価係数
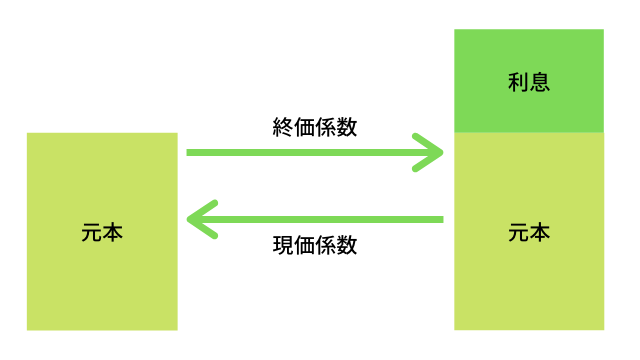
現価係数とは、一定期間後に一定金額に達するために必要な元本を求める場合に用いる係数です。
次のような場合に現価係数を利用できます。
- 10年後に自宅をリフォームする資金500万円を年率1.5%の複利運用で準備したい場合、現時点で用意すべき手元資金の金額を計算する。
読み方
現価係数の読み方は「げんかけいすう」です。
英語
英語では現価係数のことを「present value interest factor」といい、PVIFと略されます。
求め方
現価係数は次の計算式によって求めます。
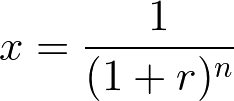
ここで、r は利率、n は年数を表わします。現価係数の求め方は、終価係数の逆数になっています。
一覧
現価係数の一覧表は次のとおりです。
| 期間 | 利率 | ||||
|---|---|---|---|---|---|
| 1% | 2% | 3% | 4% | 5% | |
| 1年 | 0.9901 | 0.9804 | 0.9709 | 0.9615 | 0.9524 |
| 2年 | 0.9803 | 0.9612 | 0.9426 | 0.9246 | 0.9070 |
| 3年 | 0.9706 | 0.9423 | 0.9151 | 0.8890 | 0.8638 |
| 4年 | 0.9610 | 0.9238 | 0.8885 | 0.8548 | 0.8227 |
| 5年 | 0.9515 | 0.9057 | 0.8626 | 0.8219 | 0.7835 |
| 6年 | 0.9420 | 0.8880 | 0.8375 | 0.7903 | 0.7462 |
| 7年 | 0.9327 | 0.8706 | 0.8131 | 0.7599 | 0.7107 |
| 8年 | 0.9235 | 0.8535 | 0.7894 | 0.7307 | 0.6768 |
| 9年 | 0.9143 | 0.8368 | 0.7664 | 0.7026 | 0.6446 |
| 10年 | 0.9053 | 0.8203 | 0.7441 | 0.6756 | 0.6139 |
現価係数の一覧表について詳しくは、下記のページでご確認ください。
エクセル
エクセルで現価係数を求めるには、セルに次の計算式を入力します。
| A | B | C | |
|---|---|---|---|
| 1 | 年 | 1% | 2% |
| 2 | 1 | =1/(1+$B$1)^A2 | =1/(1+$C$1)^A2 |
| 3 | 2 | =1/(1+$B$1)^A3 | =1/(1+$C$1)^A3 |
| 4 | 3 | =1/(1+$B$1)^A4 | =1/(1+$C$1)^A4 |
終価係数
終価係数とは、現在の金額を複利で運用した場合の、一定期間後の金額を求める場合に用いる係数です。終価係数の読み方は「しゅうかけいすう」です。
次のような場合に終価係数を利用できます。
- 余裕資金300万円を20年間、年率2.0%で複利運用する場合、20年後の元利合計額を計算する。
読み方
終価係数の読み方は「しゅうかけいすう」です。
英語
英語では終価係数のことを「future value interest factor」といい、FVIFと略されます。
求め方
終価係数は次の計算式によって求めます。
ここで、r は利率、n は年数を表わします。終価係数の求め方は、現価係数の逆数になっています。
一覧
終価係数の一覧表は次のとおりです。
| 期間 | 1% | 2% | 3% | 4% | 5% |
|---|---|---|---|---|---|
| 1年 | 1.0100 | 1.0200 | 1.0300 | 1.0400 | 1.0500 |
| 2年 | 1.0201 | 1.0404 | 1.0609 | 1.0816 | 1.1025 |
| 3年 | 1.0303 | 1.0612 | 1.0927 | 1.1249 | 1.1576 |
| 4年 | 1.0406 | 1.0824 | 1.1255 | 1.1699 | 1.2155 |
| 5年 | 1.0510 | 1.1041 | 1.1593 | 1.2167 | 1.2763 |
| 6年 | 1.0615 | 1.1262 | 1.1941 | 1.2653 | 1.3401 |
| 7年 | 1.0721 | 1.1487 | 1.2299 | 1.3159 | 1.4071 |
| 8年 | 1.0829 | 1.1717 | 1.2668 | 1.3686 | 1.4775 |
| 9年 | 1.0937 | 1.1951 | 1.3048 | 1.4233 | 1.5513 |
| 10年 | 1.1046 | 1.2190 | 1.3439 | 1.4802 | 1.6289 |
終価係数の一覧表について詳しくは、次のページをご覧ください。
エクセル
エクセルで終価係数を求めるには、セルに次の計算式を入力します。
| A | B | C | |
|---|---|---|---|
| 1 | 年 | 1% | 2% |
| 2 | 1 | =(1+$B$1)^A2 | =(1+$C$1)^A2 |
| 3 | 2 | =(1+$B$1)^A3 | =(1+$C$1)^A3 |
| 4 | 3 | =(1+$B$1)^A4 | =(1+$C$1)^A4 |
毎年一定の金額を積み立てる計画を立てる場合に、減債基金係数や年金終価係数を用いると、必要な積立額や最終的な元利合計額を簡単に求めることができます。減債基金係数と年金終価係数について詳しくは、次の記事をご覧ください。
複利運用している資金から毎年一定額を取り崩す計画を立てる場合に、年金現価係数や資本回収係数を用いると、必要な元本や受取額を簡単に求めることができます。年金現価係数と資本回収係数について詳しくは、次の記事をご覧ください。
コメント
[…] FP試験でも、金融資産の運用に関する計算などが出題されることが多く、生活においても役に立ちます。ぜひ、押さえておきたい項目です。資金計画作成６係数終価係数、現価係数、年金終価係数、減債基金係数、資本回収係数年金現価係数 […]
「老後資金2000万円不足」報告書の内容を見ると、個人にも参考になることが書かれており、良い報告書だと感じました。
経済評論家やファイナンシャル・プランナーがよく言っているようなことを金融庁が言っただけなのに、これだけ騒動になるのは「何を言うかより、誰が言うかが大事」の典型例だと思います。
私の「老後資金2000万円不足」問題に対する見解を記事にしてみました。
関連記事 老後資金2000万円不足報告書の問題