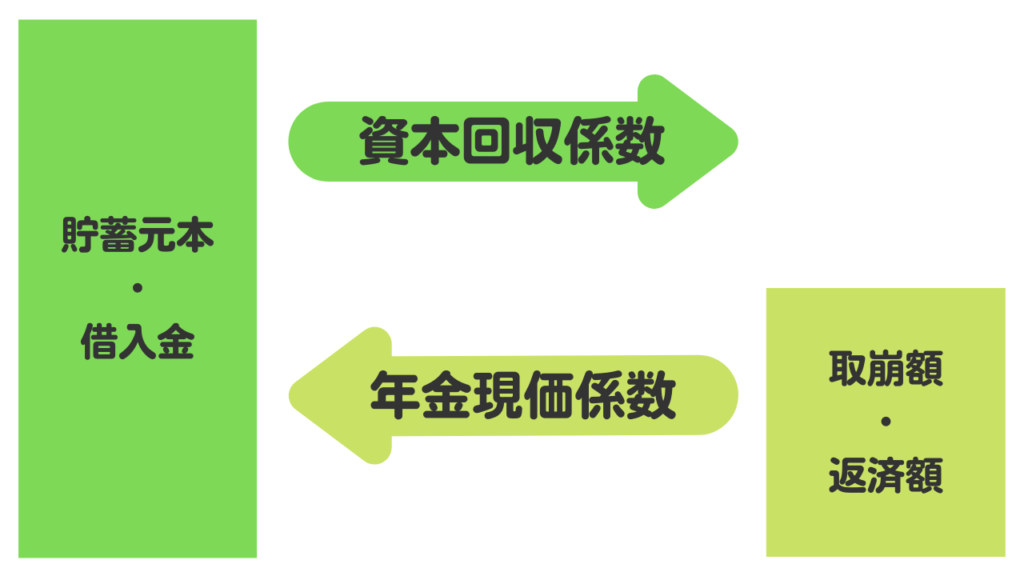
複利運用している資金から毎年一定額を取り崩す計画を立てる場合に、年金現価係数や資本回収係数を用いると、必要な元本や受取額を簡単に求めることができます。
年金現価係数
年金現価係数とは、将来の一定期間にわたって一定額を受け取るために必要な元本を計算するための係数です。
次のような場合に年金現価係数を利用できます。
- 退職してから30年間、年率1.5%で複利運用しながら、毎年50万円ずつ受け取りたい場合、退職時点で必要な金額を計算する。
覚え方
年金現価係数の覚え方は、「年金」と「現価」に分けて覚えます。
年金現価係数と年金終価係数の共通点として、どちらも「年金」というキーワードが使われています。「年金」とは、毎年一定額を積み立てたり、毎年一定額を受け取ったりすることです。
年金現価係数と現価係数の共通点として、どちらも「現価」というキーワードが使われています。「現価」とは現在の価値、すなわち貯蓄元本や現在の借入金額のことです。
つまり、年金現価係数とは、年金(毎年一定額の受取・返済)から現価(貯蓄元本・借入金)を求める計算(年金 → 現価)を行うときに使う係数ということになります。
英語
英語では年金現価係数のことを「present value interest factor of an annuity」といい、PVIFAと略されます。
計算式
年金現価係数は次の計算式で求めます。
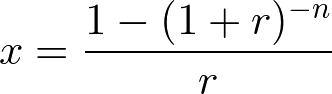
ここで、r は利率、n は年数を表わします。年金現価係数の求め方は、資本回収係数の逆数となります。
一覧
年金現価係数の一覧表は次のとおりです。
| 期間 | 利率 | ||||
|---|---|---|---|---|---|
| 1% | 2% | 3% | 4% | 5% | |
| 1年 | 0.9901 | 0.9804 | 0.9709 | 0.9615 | 0.9524 |
| 2年 | 1.9704 | 1.9416 | 1.9135 | 1.8861 | 1.8594 |
| 3年 | 2.9410 | 2.8839 | 2.8286 | 2.7751 | 2.7232 |
| 4年 | 3.9020 | 3.8077 | 3.7171 | 3.6299 | 3.5460 |
| 5年 | 4.8534 | 4.7135 | 4.5797 | 4.4518 | 4.3295 |
| 6年 | 5.7955 | 5.6014 | 5.4172 | 5.2421 | 5.0757 |
| 7年 | 6.7282 | 6.4720 | 6.2303 | 6.0021 | 5.7864 |
| 8年 | 7.6517 | 7.3255 | 7.0197 | 6.3727 | 6.4632 |
| 9年 | 8.5660 | 8.1622 | 7.7861 | 7.4353 | 7.1078 |
| 10年 | 9.4713 | 8.9826 | 8.5302 | 8.1109 | 7.7217 |
年金現価係数は、住宅ローンで借りられる金額の計算にも使えます。たとえば、月々10万円を返済する5年ローンであれば、10万円 × 12か月 × 4.8534 ≒ 582万円借りられます。
年金現価係数の一覧表について詳しくは、次のページをご覧ください。
エクセル
エクセルで年金現価係数を求めるには、セルに次の計算式を入力します。
| A | B | C | |
|---|---|---|---|
| 1 | 年 | 1% | 2% |
| 2 | 1 | =(1-(1+$B$1)^-A2)/$B$1 | =(1-(1+$C$1)^-A2)/$C$1 |
| 3 | 2 | =(1-(1+$B$1)^-A3)/$B$1 | =(1-(1+$C$1)^-A3)/$C$1 |
| 4 | 3 | =(1-(1+$B$1)^-A4)/$B$1 | =(1-(1+$C$1)^-A4)/$C$1 |
資本回収係数

現在保有している資金(元金)を一定の利率によって複利運用しながら毎年一定金額を一定の期間にわたり取り崩していくときの毎年の取崩し金額を計算する場合、資金(元金)に乗じる係数は、資本回収係数である。
6つの係数の中で唯一「取り崩し」というキーワードが登場します。元金を取り崩すことは、資本を回収することと覚えるとよいでしょう。
英語
英語では資本回収係数のことを「capital recovery factor」といい、CRFと略されます。
計算式
資本回収係数は次の計算式で求めます。
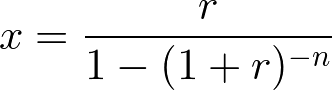
ここで、r は利率、n は年数を表わします。資本回収係数の求め方は、年金現価係数の逆数となります。
一覧
資本回収係数の一覧表は次のとおりです。
| 期間 | 利率 | ||||
|---|---|---|---|---|---|
| 1% | 2% | 3% | 4% | 5% | |
| 1年 | 1.0100 | 1.0200 | 1.0300 | 1.0400 | 1.0500 |
| 2年 | 0.5075 | 0.5150 | 0.5226 | 0.5302 | 0.5378 |
| 3年 | 0.3400 | 0.3468 | 0.3535 | 0.3603 | 0.3672 |
| 4年 | 0.2563 | 0.2626 | 0.2690 | 0.2755 | 0.2820 |
| 5年 | 0.2060 | 0.2122 | 0.2184 | 0.2246 | 0.2310 |
| 6年 | 0.1725 | 0.1785 | 0.1846 | 0.1908 | 0.1970 |
| 7年 | 0.1486 | 0.1545 | 0.1605 | 0.1666 | 0.1728 |
| 8年 | 0.1307 | 0.1365 | 0.1425 | 0.1485 | 0.1547 |
| 9年 | 0.1167 | 0.1225 | 0.1284 | 0.1345 | 0.1407 |
| 10年 | 0.1056 | 0.1113 | 0.1172 | 0.1233 | 0.1295 |
資本回収係数の一覧表について詳しくは、次のページをご覧ください。
エクセル
エクセルで資本回収係数を求めるには、セルに次の計算式を入力します。
| A | B | C | |
|---|---|---|---|
| 1 | 年 | 1% | 2% |
| 2 | 1 | =$B$1/(1-(1+$B$1)^-A2) | =$C$1/(1-(1+$C$1)^-A2) |
| 3 | 2 | =$B$1/(1-(1+$B$1)^-A3) | =$C$1/(1-(1+$C$1)^-A3) |
| 4 | 3 | =$B$1/(1-(1+$B$1)^-A4) | =$C$1/(1-(1+$C$1)^-A4) |
資本回収係数は、住宅ローンの繰り上げ返済によって月々の返済額がいくら減るのかを計算するのにも使えます。
たとえば、住宅ローンの残りが5年で金利が1.0%の場合、100万円を繰り上げ返済すると、月々の返済額が17,166円(100万円 × 0.2060 ÷ 12か月)減ります。
元本を複利で運用する計画を立てる場合に、現価係数や終価係数を用いると、必要な元本や最終的な元利合計額を簡単に求めることができます。現価係数と終価係数について詳しくは、次の記事をご覧ください。
毎年一定の金額を積み立てる計画を立てる場合に、減債基金係数や年金終価係数を用いると、必要な積立額や最終的な元利合計額を簡単に求めることができます。減債基金係数と年金終価係数について詳しくは、次の記事をご覧ください。

コメント