毎年一定の金額を積み立てる計画を立てる場合に、減債基金係数や年金終価係数を用いると、必要な積立額や最終的な元利合計額を簡単に求めることができます。
減債基金係数
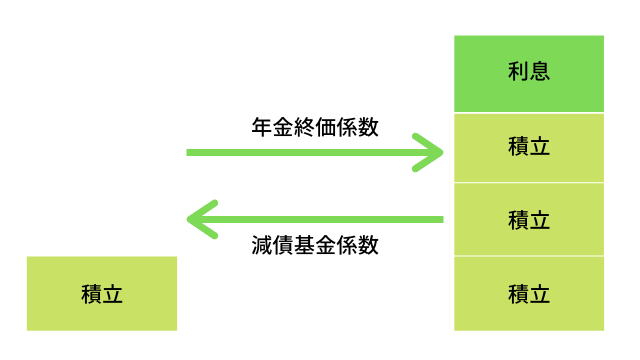
減債基金係数とは、一定期間後に一定金額を用意するための、毎年の積立額を計算するための係数です。
覚え方
見慣れない言葉かもしれませんが、減債基金とは、借金の返済に充てるための資金を積み立てておく基金のことです。個人の住宅ローンの場合は、借りたお金の一定額を毎月返済します。一方、地方公共団体が地方債を発行することにより借り入れた借金は、満期日に一括償還(返済)します。満期日が来るまでの間に、償還財源を積み充てる基金を設置して、満期日に備えるようにしています。
川崎市 (2020) 減債基金ってどうして必要なの?
償還期日と償還金額が決まっていて、毎年いくらの減債基金を積み立てればよいのかを計算するときに使うのが減債基金係数です。
借金の一括返済の他にも、住宅や車などの高額な物を購入するために積み立てる金額を求める際にも、減債基金係数を使うことができます。たとえば、次のような場合に減債基金係数を利用できます。
- 年率2.0%で複利運用しながら、5年後に自家用車を買い替える資金300万円を準備したい場合、必要な毎年の積立額を計算する。
読み方
減債基金係数の読み方は「げんさいききんけいすう」です。
英語
英語では減債基金係数のことを「sinking fund factor」といい、SFFと略されます。
計算式
減債基金係数は次の計算式で求めます。
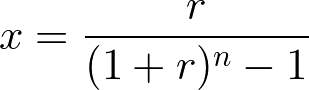
ここで、r は利率、n は年数を表わします。減債基金係数の求め方は、年金終価係数の逆数になっています。
一覧
減債基金係数の一覧表は次のとおりです。
| 期間 | 利率 | ||||
|---|---|---|---|---|---|
| 1% | 2% | 3% | 4% | 5% | |
| 1年 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 2年 | 0.4975 | 0.4950 | 0.4926 | 0.4902 | 0.4878 |
| 3年 | 0.3300 | 0.3268 | 0.3235 | 0.3203 | 0.3172 |
| 4年 | 0.2463 | 0.2426 | 0.2390 | 0.2355 | 0.2320 |
| 5年 | 0.1960 | 0.1922 | 0.1884 | 0.1846 | 0.1810 |
| 6年 | 0.1625 | 0.1585 | 0.1546 | 0.1508 | 0.1470 |
| 7年 | 0.1386 | 0.1345 | 0.1305 | 0.1266 | 0.1228 |
| 8年 | 0.1207 | 0.1165 | 0.1125 | 0.1085 | 0.1047 |
| 9年 | 0.1067 | 0.1025 | 0.0984 | 0.0945 | 0.0907 |
| 10年 | 0.0956 | 0.0913 | 0.0872 | 0.0833 | 0.0795 |
減債基金係数の一覧表について詳しくは、次のページをご覧ください。
エクセル
エクセルで減債基金係数を求めるには、セルに次の計算式を入力します。
| A | B | C | |
|---|---|---|---|
| 1 | 年 | 1% | 2% |
| 2 | 1 | =$B$1/((1+$B$1)^A2-1) | =$C$1/((1+$C$1)^A2-1) |
| 3 | 2 | =$B$1/((1+$B$1)^A3-1) | =$C$1/((1+$C$1)^A3-1) |
| 4 | 3 | =$B$1/((1+$B$1)^A4-1) | =$C$1/((1+$C$1)^A4-1) |
年金終価係数

年金終価係数とは、毎年一定金額を積み立てた場合の、一定期間後の元利合計を求める場合に用いる係数です。
読み方
年金終価係数の読み方は「ねんきんしゅうかけいすう」です。
覚え方
年金終価係数の覚え方は、「年金」と「終価」に分けて覚えます。
年金終価係数と年金現価係数の共通点として、どちらも「年金」というキーワードが使われています。「年金」とは、毎年一定額を積み立てたり、受け取ったり、返済することです。
年金終価係数と終価係数の共通点として、どちらも「終価」というキーワードが使われています。「終価」とは最終的な価額、すなわち元利合計額のことです。
つまり、年金終価係数とは、年金(毎年一定額の積立)から終価(元利合計価額)を求める計算(年金 → 終価)を行うときに使う係数ということになります。
計算式
年金終価係数は次の計算式によって求めます。
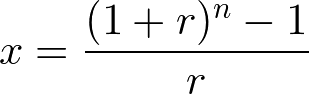
ここで、r は利率、n は年数を表わします。年金終価係数の求め方は、減債基金係数の逆数になっています。
一覧
年金終価係数の一覧表は次のとおりです。
| 期間 | 利率 | ||||
|---|---|---|---|---|---|
| 1% | 2% | 3% | 4% | 5% | |
| 1年 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 2年 | 2.0100 | 2.0200 | 2.0300 | 2.0400 | 2.0500 |
| 3年 | 3.0301 | 3.0604 | 3.0909 | 3.1216 | 3.1525 |
| 4年 | 4.0604 | 4.1216 | 4.1836 | 4.2465 | 4.3101 |
| 5年 | 5.1010 | 5.2040 | 5.3091 | 5.4163 | 5.5256 |
| 6年 | 6.1520 | 6.3081 | 6.4684 | 6.6330 | 6.8019 |
| 7年 | 7.2135 | 7.4343 | 7.6625 | 7.8983 | 8.1420 |
| 8年 | 8.2857 | 8.5830 | 8.8923 | 9.2142 | 9.5491 |
| 9年 | 9.3685 | 9.7546 | 10.1591 | 10.5828 | 11.0266 |
| 10年 | 10.4622 | 10.9497 | 11.4639 | 12.0061 | 12.5779 |
年金終価係数の一覧表について詳しくは、次のページをご覧ください。
エクセル
エクセルで年金終価係数を求めるには、セルに次の計算式を入力します。
| A | B | C | |
|---|---|---|---|
| 1 | 年 | 1% | 2% |
| 2 | 1 | =((1+$B$1)^A2-1)/$B$1 | =((1+$C$1)^A2-1)/$C$1 |
| 3 | 2 | =((1+$B$1)^A3-1)/$B$1 | =((1+$C$1)^A3-1)/$C$1 |
| 4 | 3 | =((1+$B$1)^A4-1)/$B$1 | =((1+$C$1)^A4-1)/$C$1 |
元本を複利で運用する計画を立てる場合に、現価係数や終価係数を用いると、必要な元本や最終的な元利合計額を簡単に求めることができます。現価係数と終価係数について詳しくは、次の記事をご覧ください。
複利運用している資金から毎年一定額を取り崩す計画を立てる場合に、年金現価係数や資本回収係数を用いると、必要な元本や受取額を簡単に求めることができます。年金現価係数と資本回収係数について詳しくは、次の記事をご覧ください。
コメント